샘플룸이란?
가능한 출력 목록입니다. 예를 들어, 주사위를 굴렸을 때 주사위의 패턴 공간은 1 2 3 4 5 6입니다.
목록은 상호 배타적이어야 하며 전체적으로 포괄적이어야 합니다.
설명하기 쉬운
상호 배타적: 동전에서 동전의 앞면과 뒷면이 동시에 나타나지 않아야 합니다.
총체적으로 철저한: 누락되지 않아야 합니다. 즉, 모든 숫자를 더하면 전체 집합을 얻게 됩니다.
샘플 공간: 이산 예(샘플 공간이 이산인 경우)
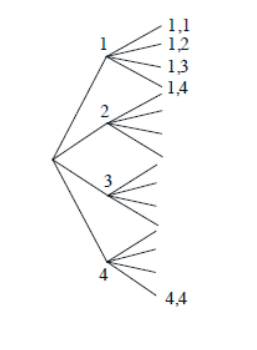
두 개의 정사면체 큐브가 있으면 어떻게 됩니까?
샘플 공간은 {1,1}, {1,2}…{4,4}입니다.
순차적으로 쓸 수도 있습니다.
샘플 공간: 연속 샘플(샘플 공간이 연속인 경우)
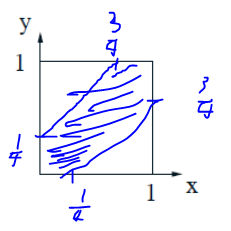
샘플 공간 = {(x,y) | 0<=x,y<=1}인 경우,
이벤트 = {(x,y) | 0 <= x, y <= 1, |xy| <= 1/4 }
이벤트의 확률은 얼마입니까?
지역별로 구매가 가능합니다.
확률 공리
1. 비음성: P(A) >= 0 무조건 확률은 0보다 커야 합니다.
2. 정규화 P(샘플 공간) = 1 모든 확률의 합은 1이어야 합니다.
3. 가산성: AnB = n(0)인 경우 P(AuB) = P(A) + P(B) 교차가 없으면 두 세트를 추가할 수 있음을 의미합니다.
확률 법칙: 유한 표본 공간의 예
사면체 정육면체를 두 번 굴립니다.
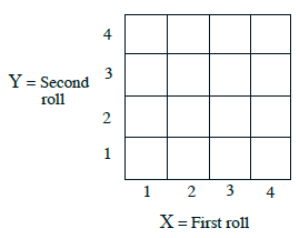
P((X,Y)는 (1,1) 또는 (1,2)) = 2/16% 두 제곱이므로
P({X = 1}) = 4/16 % 1 X가 1일 짝수 확률
P(X + Y는 홀수) = 8/16 % X+Y가 홀수이면 8칸
P(min(X,Y) = 2) % X,Y의 최소값이 2일 때
이산 통일법
모든 케이스의 확률이 같으면 P(A) = (A의 요소 수 / 총 샘플 포인트 수)
지속적인 통일법
0에서 1까지 두 개의 숫자가 무작위로 생성되면,
P(X+Y <= 1/2)는 (0,1/2), (0,0) 및 (1/2,0)의 삼각형입니다. 너비는 1/8입니다.
P((X,Y) = (0.5,0.3)) : 포인트는 확률이 될 수 없습니다. 무한히 많은 점이 있기 때문입니다.