명제
이 논문은 인간 두뇌의 각 시냅스 세트가 고유한 작업 정보를 따로 저장하고 저장하며, 마찬가지로 신경망도 각 매개 변수에 대해 다른 작업 정보를 가지고 있다고 제안합니다. 따라서 신경망 모델 순차적으로 일 학습할 때, 현재 작업 학습 단계에서 이전 단계의 현재 매개변수에 많은 작업 정보가 포함된 경우 이전 매개변수 표현식과 크게 다르지 않도록 업데이트합니다.. 이 논문은 어떤 매개변수가 많은 과거 정보를 기억하고 각 매개변수에 대해 확률적으로 근사합니다. 대략적인 확률 분포표준 편차의 크기에 의해 결정됩니다. 이 시점에서 표준 편차의 크기는 새로 도입된 정규화 항에 대한 벌점 역할을 합니다. 현재 매개변수가 이전 매개변수 표현식에서 벗어나는 것을 방지하는 정도그러므로 결정하다 이전 단계에서 현재 매개변수가 작업 정보를 많이 포함하고 있는 경우 정규화 항에 무거운 페널티를 부과하여 이전 매개변수 표현과 거의 다르지 않습니다..
논문에서 얻을 핵심 포인트
“새로운 정규화 기술을 도입하여 치명적인 망각 문제를 해결하는 확률적 접근 방식은 무엇입니까?”
학위 논문의 핵심 내용
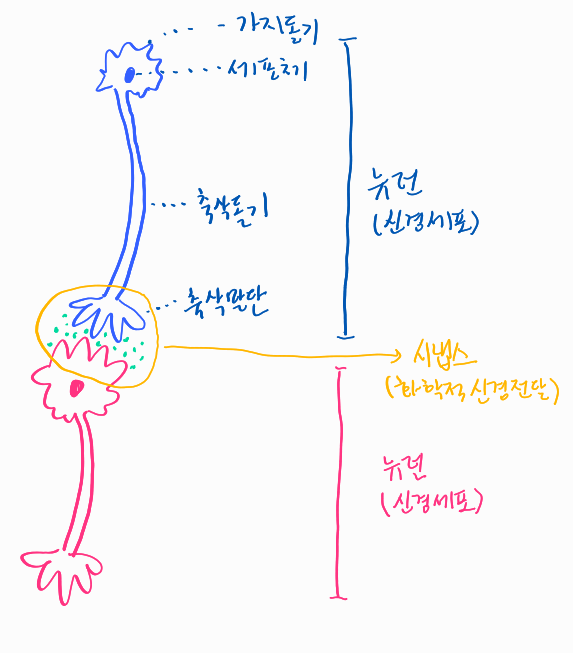
1. 인간과 동물이 끊임없이 지식을 습득할 수 있었던 이유
1. 새로운 지식을 학습하면 뉴런의 수상돌기 수가 증가하고 시냅스가 활성화됩니다.
2. 뉴런의 수상돌기는 새로운 지식을 학습한 후에도 오랫동안 보존될 수 있습니다.
3. 이전에 학습한 지식은 암호화되어 시냅스에 저장됩니다.
4. 그러므로 수상돌기의 긴 수명은 시냅스를 오랫동안 보존할 수 있게 하여 지식이 오랫동안 저장됩니다.할수있다
5. 특정 작업 및 기술에 추가로 전문화 시냅스는 고립되어 활성화됩니다.나는 그것을 확인할 수 있습니다.

2. 논문에서 제안하는 Elastic Weight Consolidation(EWC)이란?
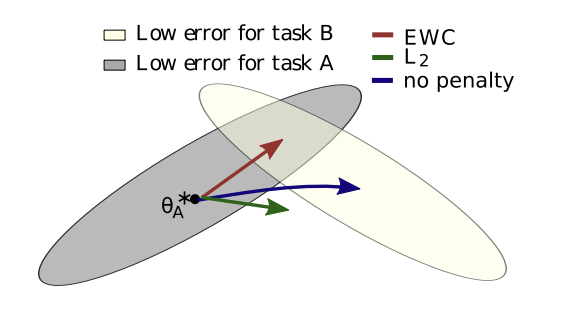
하나. EWC 태스크 A를 학습한 후 매개변수를 최적화하고 다음 태스크 B를 학습할 때 목표는 태스크 A에 대한 낮은 오류 범위에서 크게 벗어나지 않고 매개변수가 업데이트되도록 하는 것입니다(그림 1 참조).
2. 목적 함수에 페널티를 추가하여 매개변수 업데이트에 제약을 가합니다.
3. 여기서는 상대적으로 유연한 매개변수 업데이트의 속성을 탄성 스프링과 비교하고 업데이트에 대한 구속을 부과하는 것은 스프링에 추를 매달아 견고하게 고정된 것으로 표현됩니다.
4. “탄성”을 의미하는 탄성이라는 단어와 위의 “시냅스는 특정 작업과 지식에 특화되어 있기 때문에 고립되어 활성화된다”는 점을 적용함으로써, “탄성 무게 강화” 이것이 새로운 방법이 논문에서 명명된 방식입니다.
3. 최적화 문제에 대한 확률론적 접근.
1. (주어진 데이터 내에서) 확률적으로 파라미터 최적화 고려 “손실 최소화” 가능성이 더 높은 파라메트릭 표현 찾기동일시될 수 있다
2. 이것은 P(theta | data)로 표현될 수 있다: 주어진 데이터의 theta의 사후 확률 “매개변수 최적화는 세타가 주어진 데이터의 사후 우도를 최대화하는 세타를 찾는 문제입니다.“대신 호출할 수 있습니다.
3. 그리고 P(theta | data)는 Bayes rule과 log에 의해 계산된다. 로그 P(세타 | 데이터) = 로그 P(데이터 | 세타) + 로그 P(세타) – 로그 P(데이터) 데이터가 이전에 실행된 작업 A와 현재 실행 중인 작업 B로 나뉘는 방정식으로 표현할 수 있습니다. = logP(데이터_B | 세타) + log P(세타 | 데이터_A) – 로그 P(데이터_B) 새롭다고 표현할 수 있다
4. 주어진 데이터에서 “손실 최소화” 확률이 높은 세타 찾기
1. EWC의 학습 목표는 다음과 같습니다. “로그 P(세타 | 데이터) 최대화” 모두.
2. 이때 로그 P(세타 | 데이터) = 로그 P(데이터_B | 세타) + log P(세타 | 데이터_A) – 로그 P(데이터_B) 방정식을 사용하여 새로운 목적 함수를 도입하고 “목적 함수 최소화”라는 EWC의 새로운 학습 목표를 제안합니다.
3. 먼저 로그 P(데이터_B | 세타) 이다 “세타로 매개변수화된 데이터가 주어진 작업 B의 확률‘, ‘쎄타의 확률’과 같습니다.
4. 그리고 “대수 확률(L) 최대화 = 비용 함수(J) 최소화”(1) 로그 P(데이터_B | 세타) 최소화 J_B(세타) 표현
(1) 내용 참고: 스탠포드 CS229 강의 3
5. 위에서 정의한 방정식을 보면, 과거 정보(즉, 작업 A에 대한 정보)를 포함하는 유일한 용어입니다. 로그 P(세타 | 데이터_A): Task A의 데이터가 주어진 세타의 사후확률은 1이다. EWC의 본질인 “파라미터에 가중치를 부여하는 행위”(두 번째 소절에서 언급)는 해당 용어에서 알 수 있습니다.
6. 라플라스 근사(2) 사후 확률 함수는 (다변량) 가우시안 분포로 근사화될 수 있습니다.
7. 이때 평균 태스크 A에서 최적화된 매개변수(=theta_A*), 공분산 행렬 ~이다 역 피셔 정보 행렬 F(3) 에 해당합니다
(2) 콘텐츠 공지: https://bookdown.org/rdpeng/advstatcomp/laplace-approximation.html
(3) 세타 크기가 n이면 F 크기는 nxn입니다.
※ 라플라스 근사 L2 공간에 정의된 함수 g(x)의 면적을 계산하는 문제를 해결합니다. Taylor 급수로 g(x)를 가우시안 분포에 근사하면 Argmax를 찾는 것이 문제(최적화 문제)가 됩니다. 그리고 대략적인 가우시안 분포의 평균은 “x_0“, 분산은 “-h”(x_0)^-1“는 (h = 로그 g)
※ 어부 정보 라플라스 근사에 필요한 유일한 정보를 의미합니다. Fisher 정보 행렬 F는 (다변수인 경우)”– d/dx_알파 h(x) * d/dx_베타 h(x)“는 근사(다변량) 가우시안 분포의 공분산 행렬 C의 역과 같습니다. (F ≡ C^-1) (내용 참조)
8일. Fisher 정보 행렬 F의 대각선(4) 대략적인 가우시안 분포 내에서 관찰된 세타의 평균값 사이의 폭을 나타냅니다(즉, 세타가 평균을 얼마나 제한하는지). F의 대각선 크기가 클수록 더 좁고/더 제한적입니다.의미
9. 역관계인 공분산행렬을 보면 공분산행렬의 대각선, 즉 “표준편차”가 작을수록 좁고/제한적으로 볼 수 있다.
10. 가우스 분포 곡선의 좁은 폭 “확률 모드가 큽니다”즉 Theta는 “손실 최소화”의 최대 확률이 높습니다.수단
(4) F의 대각선만 고려하는 이유: 대각선을 제외한 나머지는 theta_i와 theta_j 사이에 어떤 상관관계가 있는지를 나타낸다. 그러나 가우시안 분포 내에서 너비를 찾으려고 하기 때문에 대각선만 고려합니다.
11. 따라서 F의 대각선이 큰 theta_i는 새로운 작업 B가 학습되더라도 어떻게든 theta_A,i*에 가깝게 렌더링되어야 합니다.
12. F의 대각선은 목적함수이다. J_B(세타) 정규화 용어 추가 (theta_i – theta_A,i*) 에 대한 형벌로 작용
13. 결과적으로 “로그 P(세타 | 데이터) 최대화” EWC 학습 목표 “다음 목적 함수 최소화(그림 2 참조)”최적화 문제를 해결하기 위해.
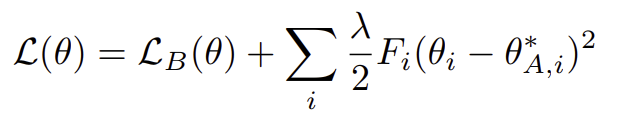
14. 새로 정의된 목적 함수 L(theta)는 로그 P(데이터_B | 세타) 손실 함수로, 로그 P(세타 | 데이터_A) 변형되어 정규화 용어로 사용됩니다.
15. 그리고 기대값 전파(expectation propagation)와 유사하다고 하는데, 기대값 = 평균값 = 세타*로 태스크가 차례로 실행되는 동안 이전 태스크의 세타*가 변경되지 않고 다음 태스크로 이월되어 영향을 준다는 것을 의미합니다. .
16. 정규화 용어에서 람다는 세타와는 별개로 작업 자체만 보고 현재 작업을 이전 작업과 비교하여 서로 얼마나 관련이 있는지(= 이전 작업이 작업 실행에 얼마나 중요한지 보여줍니다. 현재 작업). ). 서로 관련성이 높을수록 람다 크기가 커지므로 theta는 이전 theta*에 근접합니다.
* L(theta)가 최적화 문제 해결에 적합한 이유:
(a) L(세타)를 최소화합니다. = P(세타 | 데이터)를 최대화합니다.
(b) P(세타 | 데이터)를 최대화합니다. = “손실 최소화” 확률을 높이는 세타를 찾습니다.
(씨) “손실 최소화” 가능성을 높이는 세타를 찾으십시오. = 해당 세타만큼 “손실 최소화”.
(d) 결국 최적화 문제를 해결하는 것으로 귀결됩니다.
이미지 출처:
– https://arxiv.org/pdf/1612.00796.pdf
최종 업데이트: 2023. 03. 05.
임태준 작사

.png?type=w800)